Actions sur le document
Principe de la division
Diviseur à un chiffre
La méthode pour la division d'un nombre par un diviseur à un chiffre que nous allons décrire est identique sur le principe à celle de la division posée. On commence par écrire le dividende à partir de la droite puis le diviseur en laissant quatre tiges vacantes.
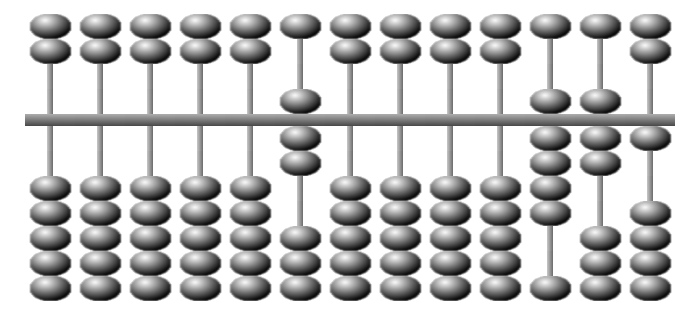
Position initiale pour le calcul du quotient de 971 par 7.
On détermine le quotient entier du premier ou des deux premiers chiffres du dividende par le diviseur. Dans le premier cas, on marque celui-ci à gauche du dividende en laissant une tige libre. Dans le second cas, on marque celui-ci immédiatement à gauche du dividende. Enfin, on retire au dividende le produit de ce quotient par le diviseur. Et ainsi de suite...
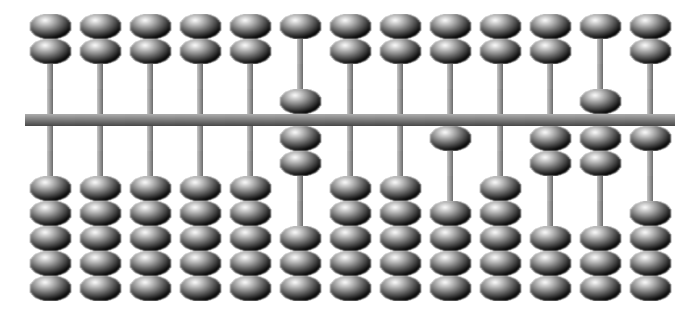
Le premier chiffre est 1. On retire 7.
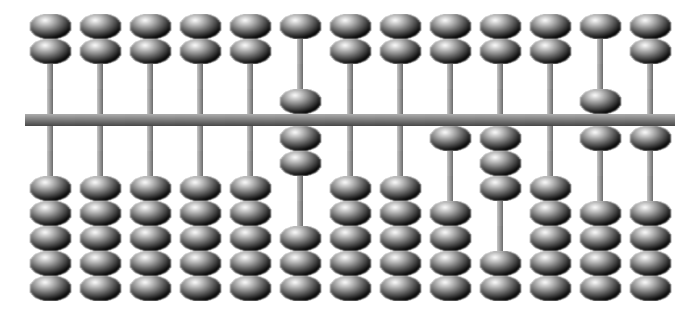
Le deuxième chiffre est 3. On retire 21.
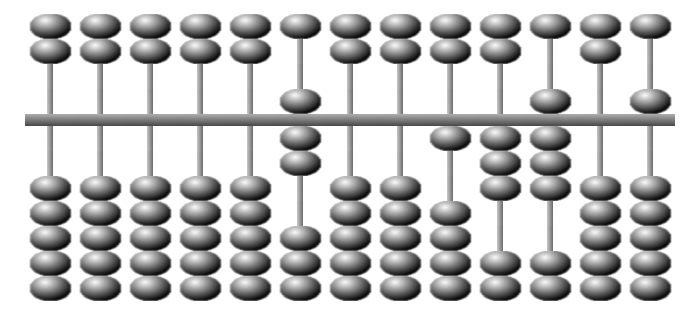
Le troisième chiffre est 8. On retire 56.
971 = 138 × 7 + 5.
La position finale d'une division correspond à la position initiale de la multiplication inverse, ce qui révèle utile lorsqu'on effectue une vérification.
Diviseur à plusieurs chiffres
Pour un diviseur à plusieurs chiffres, on se contente d'utiliser le premier chiffre du diviseur pour choisir les chiffres du quotient. Lorsque la quantité à soustraire du dividende se révèle trop petite ou trop grande, on corrige a posteriori le chiffre concerné. Voici, par exemple, le calcul du quotient de 5 607 par 63.
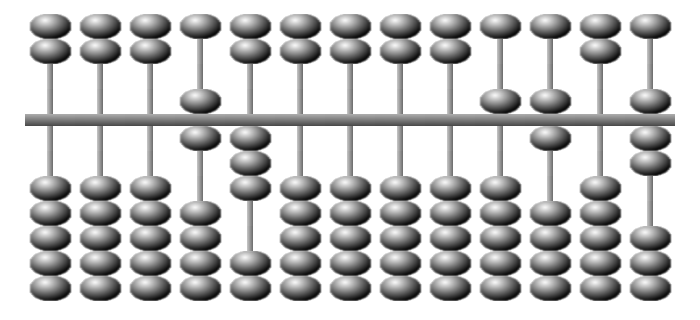
Position initiale.
On choisit 9 comme premier chiffre du quotient. On retire 6 × 9 = 54 Ã partir de la 4e tige.
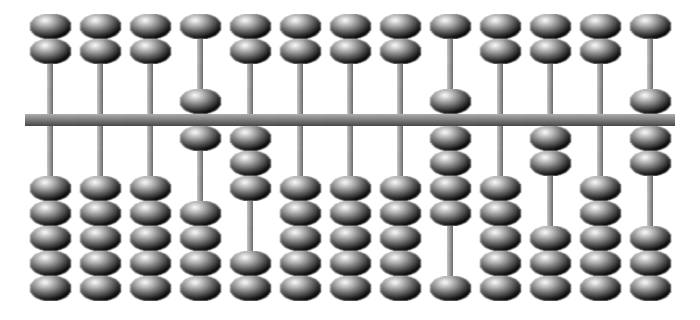
On retire 6 × 9 = 54.
Il n'est pas possible de retirer 3 × 9 = 27 Ã partir de la 3e tige. On diminue donc de 1 le premier chiffre du quotient et l'on ajoute 6 sur la 3e tige, puis on retire 3 × 8 = 24.
Correction du premier chiffre.
On retire 3 × 8 = 24.
On choisit 9 comme second chiffre du quotient. On retire 6 × 9 = 54 Ã partir de la 3e tige, puis on retire 3 × 9 = 27 Ã partir de la 2e tige.
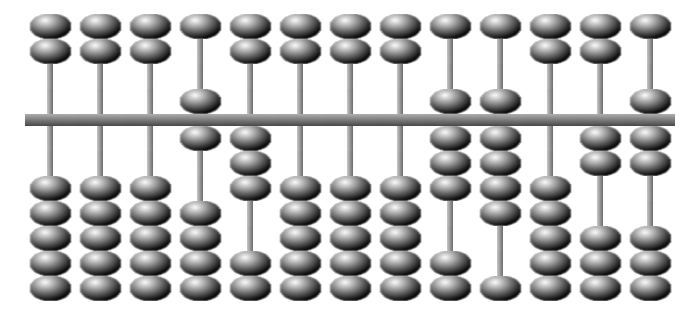
On retire 6 × 9 = 54 ...
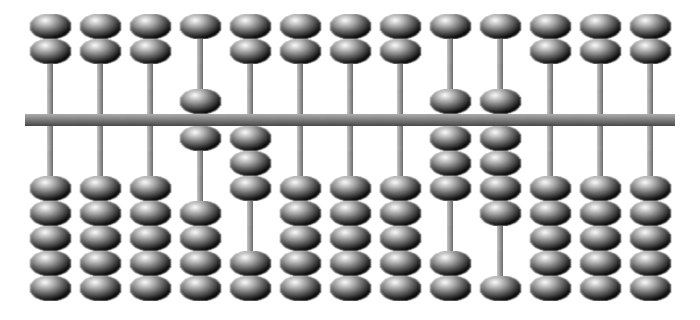
... puis on retire 3 × 9 = 27.
Le reste est nul. On lit le résultat : 5 607 ÷ 63 = 89.
L'utilisation du seul premier chiffre du diviseur pour la détermination des chiffres du quotient diminue l'effort mental consenti. Cela contribue à accélérer le calcul en dépit du recours à d'éventuelles corrections.
